Konstruktion eines Dreiecks um die Winkelhalbierenden
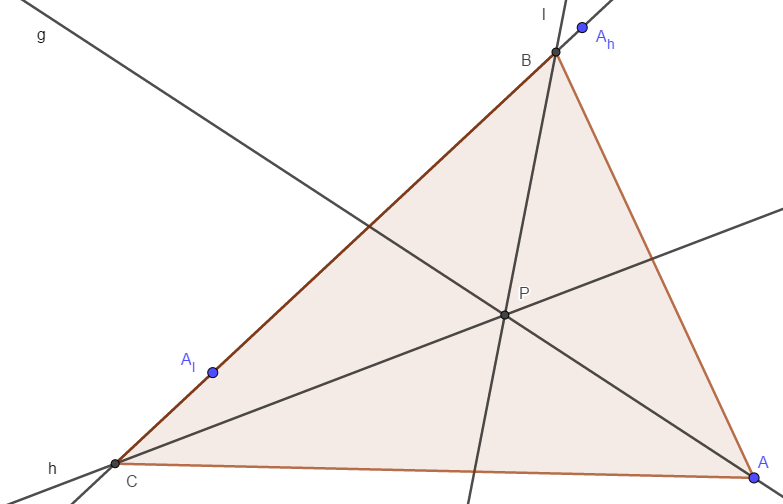
Gesucht ist ein Dreieck △ABC, zu welchem die Geraden g, h, l die Winkelhalbierenden sind.
Dazu schlägt Maximilian die folgende Konstruktion vor:
- Wähle einen Punkt A auf g, der von P verschieden ist.
- Der Spiegelpunkt von A an h sei Ah, der Spiegelpunkt von A an l sei Al.
- Die Schnittpunkte der Geraden g(Ah;Al) mit h bzw. l seien B bzw. C.
- △ABC ist das gesuchte Dreieck.
Ist diese Konstruktion eigentlich (immer) durchführbar?
Prüfe dafür jeden Schritt und argumentiere!
Schritt 1: Ja, da die Wahl von A auf g\P irrelevant ist, weder Entfernung noch Richtung ändern das Ergebnis.
Schritt 2: Ja, da die Spiegelung eindeutig ist. Und da wir nicht auf einem Blatt Papier arbeiten, sondern einer unendlichen Ebene, ist dies auch immer möglich.
Schritt 3: Ja, denn da sich h und l nur in P schneiden, sind sie nicht identisch.
Deshalb kann auch g(A_h;A_l) nicht identisch zu h oder l sein, also existieren eindeutige Schnittpunkte.
https://www.tutory.de/entdecken/dokument/geodid-serie-5-a3
Als letztes überprüfen wir noch den 4. Schritt:
Liefert die Konstruktion tatsächlich das gesuchte Dreieck?
Man bezeichne den Lotfußpunkt von dem Lot auf h durch A mit
Fh den Fußpunkt vom Lot auf l durch A mit Al und g(Ah, Al) ∩ g = : {Fg}.
Um zu zeigen, dass g, h & l tatsächlich
Winkelhalbierende sind, muss gelten:
(i) β1 = β2 (ii) γ1 = γ2 (iii) α1 = α2
Beweis:
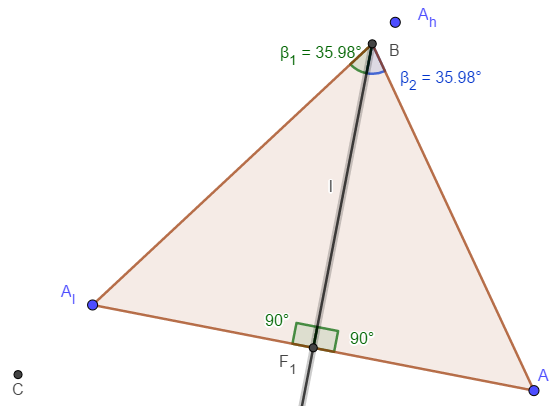
(i) β1 = β2
Man betrachte △BAlFl und △BAFl.
Diese haben folgendes gemeinsam:
- ∣AlFl∣=∣AFl∣
- ∣∠BFlAl∣=∣∠BFlA∣ = 90°
- BFl als gemeinsame Seite
Mit dem Kongruenzsatz SWS folgt nun
∣△BAlP∣≅∣△BAP∣
⇒β1=β2.
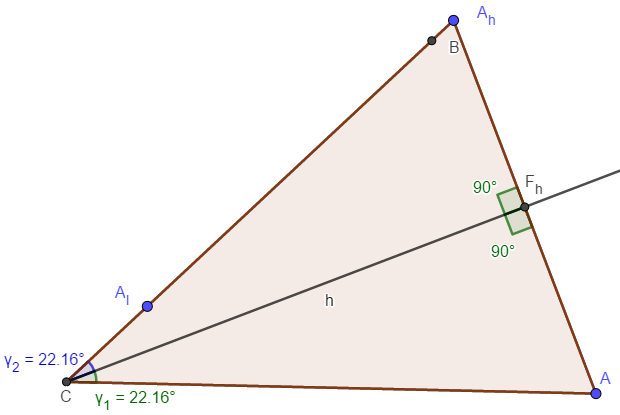
(ii) γ1 = γ2
Tipp: Suche wie bei (i) 2 geeignete Dreiecke,
beweise analog und zeichne eine Skizze!
Man betrachte △CFhAh & △CAFh.
Diese haben folgendes gemeinsam:
- ∣AhFh∣=∣FhA∣
- ∣∠CFhAh∣=∣∠CFhA∣ = 90°
- CFh als gemeinsame Seite
SWS ⇒∣△CFhAh∣≅∣△CAFh∣
⇒γ1=γ2.
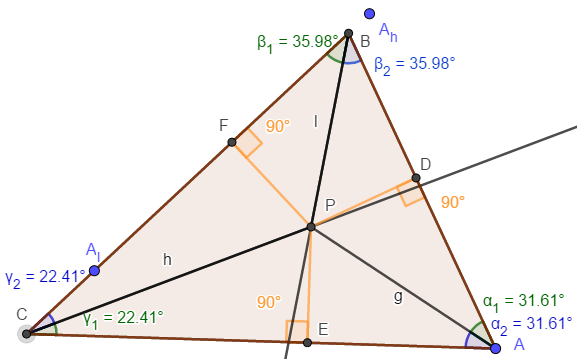
(iii) α1 = α2
Seien D, E und F Lotfußpunkte der Lote
auf AB,AC bzw. BC durch P.
Das □ADPE können wir über die beiden
gegenüberliegenden rechten Winkel und die
gleichlangen Seiten DP,PE , sowie EA,AC als Drachen identifizieren, mit g als der
Diagonale, welche die andere halbiert.
Also ist g auch die Winkelhalbierende für
∠DPE und ∠EAD=α
⇒α1=α2.
https://www.tutory.de/entdecken/dokument/geodid-serie-5-a3


